Matematikos programa

Ką turi žinoti 11-tokas (A lygis)

Skaičiai ir skaičiavimai

Skaičių aibės

Nagrinėjama realiųjų skaičių aibės struktūra.

Pateikiami baigtinių ir begalinių; diskrečiųjų ir tolydžiųjų (intervalų) skaičių aibių pavyzdžiai.

Mokoma(si) reiškiniu užrašyti natūraliųjų skaičių, kuriuos dalijant iš nurodyto natūraliojo skaičiaus

n⋅d+r, n∈N.

Apibrėžiama aibių sąjunga, sankirta ir skirtumas. Atliekami veiksmai su aibėmis. Praktikuojamasi veiksmus su aibėmis vaizduoti Veno diagramomis.

Realiojo skaičiaus modulis

Apibrėžiama realiojo skaičiaus modulio sąvoka ir paaiškinama jo geometrinė prasmė.

Braižomas y=∣x∣ grafiko eskizas.

Mokoma(si) užrašyti lygties ∣x∣=a ir nelygybės ∣x∣⋚a (a∈R) sprendinių aibes.

Pavyzdžiais pagrindžiamos modulio (ir veiksmų su moduliais) savybės:

∣−a∣=∣a∣, ∣a∣²=a², ∣a−b∣=∣b−a∣, ∣a⋅b∣=∣a∣⋅∣b∣, ∣a ∶ b∣=∣a∣ ∶ ∣b∣ ,

Mokoma(si) apskaičiuoti skaitinių ir raidinių reiškinių su moduliais reikšmes, traukti lyginio laipsnio šaknį iš lyginio laipsnio:

Laipsniai

Šaknys

Logaritmai

Sinusas, kosinusas ir tangentas

Modeliai ir sąryšiai

Progresijos

Funkcijos

Lygtys

Nelygybės

Geometrija ir matavimai

Plokštumos vektoriai ir veiksmai su jais

Apibrėžiamas kampas tarp vektorių. Apibrėžiama dviejų vektorių skaliarinė sandauga, mokoma(si) skaliariškai dauginti vektorius. Įrodoma, kad vektoriaus kvadratas (vektoriaus skaliarinė sandauga su pačiu savimi) yra lygus vektoriaus ilgio kvadratui. Primenama, kaip randama vektorių suma (naudojantis trikampio ir lygiagretainio taisyklėmis; paaiškinama daugiakampio taisyklė), vektorių skirtumas, vektoriaus ir skaičiaus sandauga. Mokoma(si) nurodytą daugiakampio vektorių išreikšti kitais nurodytais to daugiakampio vektoriais. Apibrėžiama ir paaiškinama dviejų vektorių skaliarinė sandauga, mokoma(si) skaliariškai dauginti vektorius, pabrėžiant, kad skaliarinės sandaugos rezultatas yra skaičius, o ne vektorius. Veiksmams su vektoriais taikomos žinomos veiksmų su skaičiais savybės:

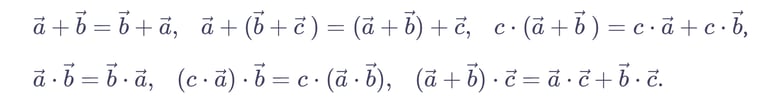
Vektoriai stačiakampėje koordinačių plokštumoje

Mokoma(si) nusakyti vektorių, nurodant jo pradžios ir pabaigos koordinates; apibrėžiant koordinačių plokštumos taško vietos vektorių ir mokantis bet kurį koordinačių plokštumos vektorių išreikšti jam lygiu taško vietos vektoriumi.

Mokoma(si) apskaičiuoti vektoriaus ilgį ir įrodyti vektoriaus ilgio formulę.

Mokoma(si) apskaičiuoti vektorių sumą, skirtumą, sandaugą su skaičiumi bei skaliarinę sandaugą, paaiškinant atliekamų veiksmų prasmingumą.

Apibrėžiami koordinačių ašių vienetiniai vektoriai ir mokoma(si) jais reikšti koordinačių plokštumos vektorius.

Apibrėžiami kolinearieji ir statmenieji vektoriai. Analizuojamos dviejų vektorių kolinearumo ir statmenumo sąlygos bei sprendžiami su šiais faktais susiję uždaviniai.